如图,被称为“天津之眼”的天津永乐桥摩天轮是一座跨河建造、桥轮合一的摩天轮.假设“天津之眼”旋转一周需要30分钟,且是匀速转动的,则经过5分钟,点B转过的角的弧度是( )

- A:
- B:
- C:
- D:
由题意可知,点B转过的角的弧度是×2π=.
下列各角中,与27°角终边相同的是( )
与27°角终边相同的角构成的集合为{α|α=27°+k·360°,k∈Z},取k=1,可得α=387°.故与27°角终边相同的是387°.
sin 45°cos 15°+cos 225°sin 15°的值为( )
sin 45°cos 15°+cos 225°sin 15°
=sin 45°cos 15°+cos(180°+45°)sin 15°
=sin 45°cos 15°-cos 45°sin 15°
=sin(45°-15°)=sin 30°=.
若sin=,则sin 2α等于( )
设β=α+,则sin β=,α=β-,
故sin 2α=sin 2=-cos 2β=2sin2β-1=-.
如果角α的终边过点P(2sin 30°,-2cos 30°),那么sin α等于( )
由题意得P(1,-),它与原点的距离为2,则sin α=-.
如图,被称为“天津之眼”的天津永乐桥摩天轮是一座跨河建造、桥轮合一的摩天轮.假设“天津之眼”旋转一周需要30分钟,且是匀速转动的,则经过5分钟,点B转过的角的弧度是( )

由题意可知,点B转过的角的弧度是×2π=.
函数y=x-2sin x(-π≤x≤π)的大致图象是( )
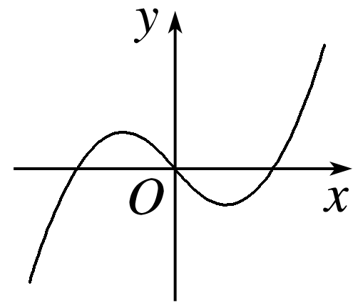
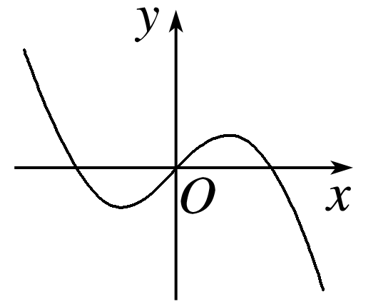
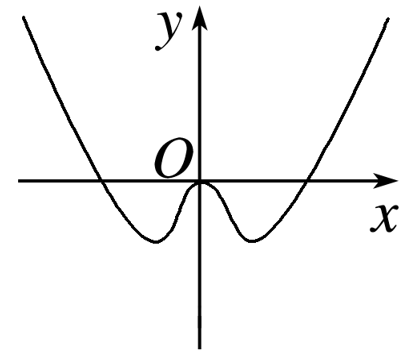
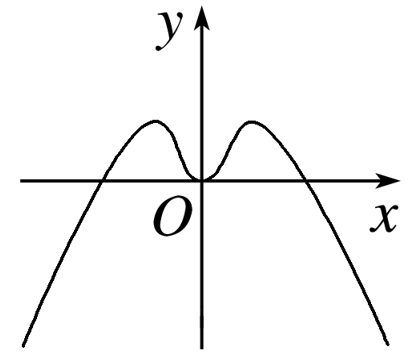
令函数f(x)=x-2sin x,
显然f(-x)=-x-2sin(-x)=-f(x),
因此函数f(x)是[-π,π]上的奇函数,图象关于原点对称,故C,D不满足;
当x=π时,y=π-2sin π=π,故B不满足,A符合题意.
若tan 2α=,则等于( )
由于=tan 2α=,故4-4tan2α=6tan α,即2-3tan α=2tan2α.
所以====2.
在△ABC中,内角A,B,C满足2sin Bcos C=sin A,则△ABC的形状为( )
2sin Bcos C=sin A=sin(B+C)=sin Bcos C+cos Bsin C,
故sin Bcos C-cos Bsin C=0,即sin(B-C)=0,
因为B,C∈(0,π),所以B=C,故△ABC为等腰三角形.
(多选)下列结论正确的是( )
选项A,-的终边与的终边相同,为第二象限角,所以A不正确;
选项B,设扇形的半径为r,r=π,所以r=3,
扇形面积为×3×π=,所以B正确;
选项C,角α的终边过点P(-3,4),根据三角函数的定义,cos α=-,所以C正确;
选项D,当角α为锐角时,0<α<,0<2α<π,所以D不正确.
(多选)如图是函数y=Asin(ωx+φ)(x∈R)在区间上的图象.为了得到这个函数的图象,只要将y=sin x(x∈R)的图象上所有的点( )
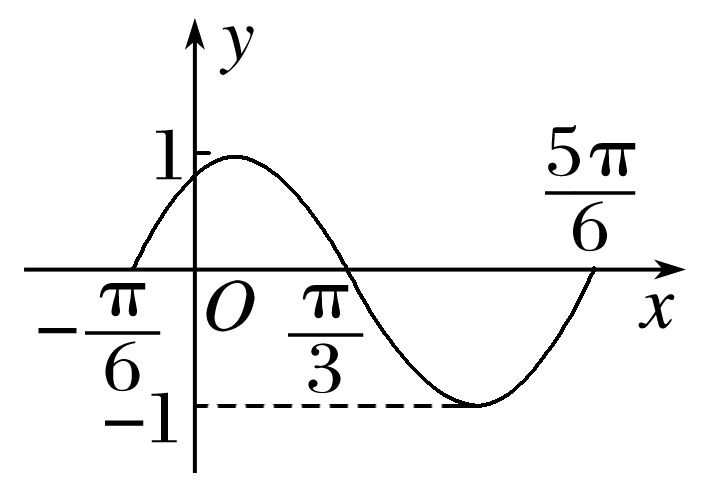
由图象知,A=1,T=π,所以ω=2,y=sin(2x+φ),将代入得sin=0,
所以φ-=kπ,k∈Z,取k=0,则φ=,
得y=sin,将y=sin x的图象向左平移个单位长度,得到函数y=sin的图象,然后将各点的横坐标缩短到原来的,纵坐标不变,得到函数y=sin的图象,故A正确,B错误,D错误;
将y=sin x各点的横坐标缩短到原来的,纵坐标不变,得到函数y=sin 2x的图象.然后向左平移个单位长度,得到函数y=sin 2=sin的图象,故C正确.
(多选)已知函数f(x)=2cos(ω>0)的最小正周期为π,则( )
对于A,因为函数f(x)=2cos(ω>0)的最小正周期为π,所以=π,可得ω=2,故A正确;
对于B,f=2cos=2cos π=-2,故B正确;
对于C,当x∈时,2x+∈,因为y=cos x在上单调递增,在上单调递减,所以f(x)在区间上不单调,故C错误;
对于D,当x∈时,2x+∈,所以cos∈,可得f(x)在区间上的值域为[1,2],故D错误.
函数f(x)=3sin的初始相位为 .
答案:
函数f(x)=3sin的初始相位为.
已知cos(α+765°)=,则cos α-sin α= .
答案:
因为cos(α+765°)=cos(α+45°+2×360°)=cos(α+45°)=cos α-sin α=,
所以cos α-sin α=.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则f(x)的单调递增区间为 .
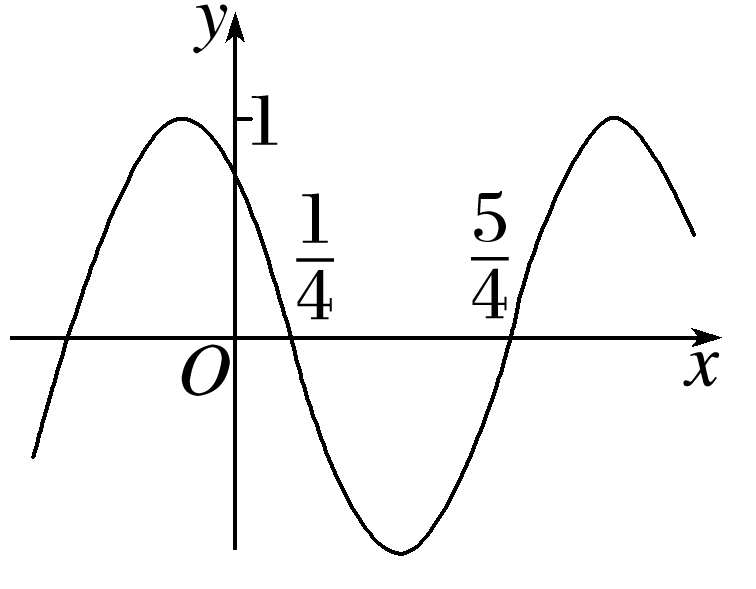
答案: ,k∈Z
由图象知T==2,所以ω=π,由五点法作图知+φ=π,即φ=,
∴f(x)=sin,
令2kπ-≤πx+≤2kπ+,k∈Z,
解得2k-≤x≤2k-,k∈Z.
∴f(x)的单调递增区间为,k∈Z.
已知sin α=,α∈.
(1)求cos α,tan α的值;
(2)求sin 2α,cos 2α的值;
(3)求cos的值.
答案: 解 (1)因为sin α=,α∈, 所以cos α=-=-,tan α=-. (2)sin 2α=2sin αcos α=-, cos 2α=cos2α-sin2α=. (3)cos=cos αcos+sin αsin=.
已知函数f(x)=sin2x-cos2x+2sin x·cos x.
(1)求f(x)的最小正周期;
(2)若f(α)=,求cos的值.
答案: 解 (1)f(x)=sin2x-cos2x+2sin xcos x=-cos 2x+sin 2x=2=2sin, ∴T=π. (2)由(1)得f(α)=2sin=, ∴sin=, ∴cos=cos 2=1-2sin2=1-=.
已知函数f(x)=sin.
(1)求函数f(x)的最大值和最小值及相应自变量x的取值集合;
(2)画出函数y=f(x)在区间上的图象.
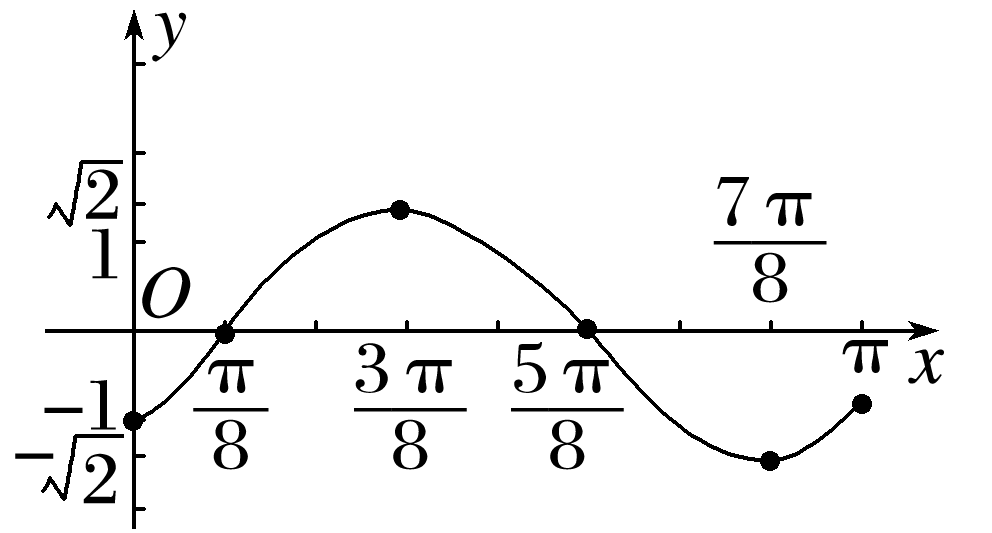
答案: 解 (1)当2x-=+2kπ,k∈Z, 即x=+kπ,k∈Z时,f(x)取到最大值, ∴f(x)取得最大值时相应自变量x的取值集合为;当2x-=-+2kπ,k∈Z, 即x=-+kπ,k∈Z时,f(x)取到最小值-, ∴f(x)取得最小值时相应自变量x的取值集合为. (2)列表: 描点、连线,f(x)的图象如图所示.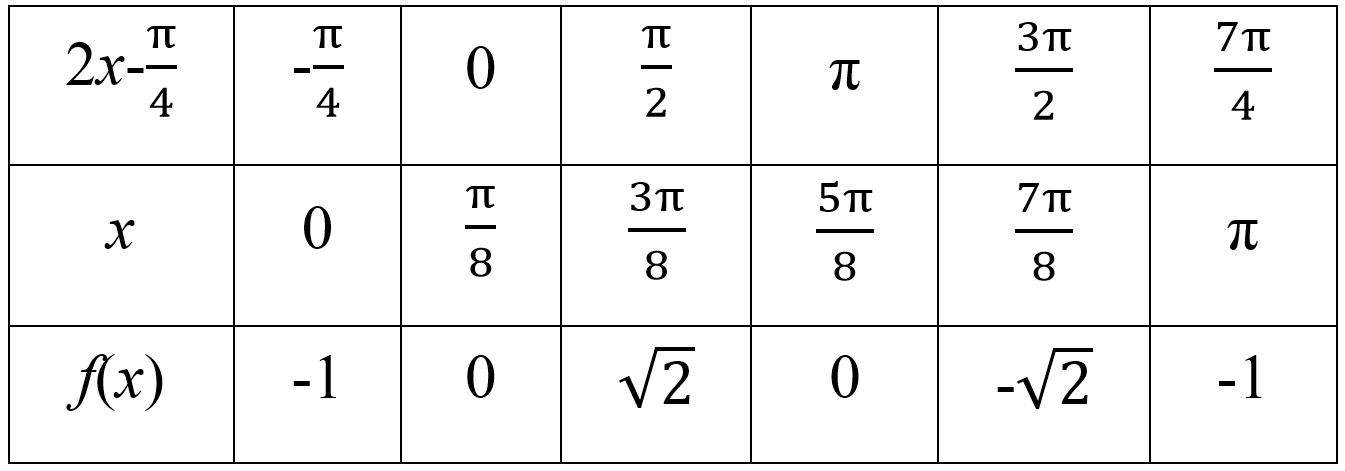
直径为8 m的水轮如图所示,水轮圆心O距离水面2 m,已知水轮沿逆时针方向匀速旋转,每分钟转动6圈,当水轮上点P从水中浮现时(图中点P0)开始计算时间.
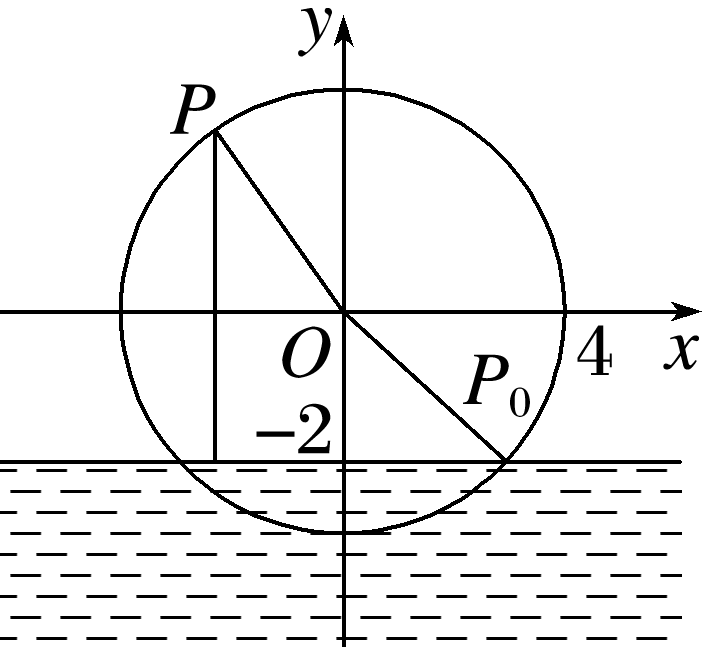
(1)将点P距离水面的高度h(m)表示为时间t(s)的函数;
(2)在水轮转动的一圈内,有多长时间点P在水面以下?
答案: 解 (1)由题意可知,ω==, 设角φ是以Ox为始边,OP0为终边的角, 由条件得h=4sin+2, 将t=0,h=0代入,得4sin φ+2=0, ∴φ=-,∴h=4sin+2. (2)由题意知4sin+2<0, 即sin<-, ∴t-∈,k∈Z. 即t∈,k∈Z, ∴10-=. ∴在水轮转动的一圈内,点P在水下时间为 s.
我们把平面直角坐标系中函数y=f(x)(x∈D)上满足x∈N*,y∈N*的点P(x,y)称为函数y=f(x)的“正格点”.
(1)请你选取一个m的值,使函数y=f(x)=sin mx(x∈R)的图象上有“正格点”,并写出函数的一个“正格点”坐标;
(2)若函数f(x)=sin mx(x∈R,m∈(1,2))与函数g(x)=lg x的图象有“正格点”交点,求m的值,并写出两个函数图象的所有交点个数;
(3)对于(2)中的m值,若函数f(x)=sin mx,x∈时,不等式logax>sin mx恒成立,求实数a的取值范围.
答案: 解 (1)取m=时,“正格点”坐标为(1,1),(5,1),(9,1)等(答案不唯一). (2)作出两个函数图象.如图, 可知函数f(x)=sin mx,x∈R,与函数g(x)=lg x的图象只有一个“正格点”交点(10,1). 则2kπ+=10m,m=π(k∈Z), 又m∈(1,2),可得m=. 根据图象可知,两个函数图象的所有交点个数为4. (3)由(2)知f(x)=sin x,x∈, 当a>1时,不等式logax>sin x不能成立; 当0<a<1时,由(2)可得loga>sin =, 则<a<1.