三角函数图像与性质

第1题 (单选题) 难度 - ：

函数的最小正周期为（）

A:
B:
C:
D:

解析:

根据公式计算直接得出结果.

由题意知，

函数的最小正周期为.

故选：C.

第2题 (单选题) 难度 - ：

函数的最小值为（）

A:
B:
C: 3
D: 4

解析:

利用余弦函数的值域算出结果.

因为，

所以，

所以最小值为，

故选：B

第3题 (单选题) 难度 - ：

函数的最小正周期为

A:
B:
C:
D:

解析:

直接利用三角函数周期公式得到答案.

函数的最小正周期为.

故选：.

【点睛】本题考查了三角函数周期，属于简单题.

第4题 (单选题) 难度 - ：

函数的定义域为（）

A:
B:
C:
D:

解析:

直接由求解即可

解：由，得，

所以函数的定义域为，

故选：C

【点睛】此题考查求正切型函数的定义域，利用了整体的思想，属于基础题.

第5题 (单选题) 难度 - ：

下列各点中，可以作为函数图象的对称中心的是（）

A:
B:
C:
D:

解析:

利用余弦函数的性质，逐项验证即可得解.

对于AC，，AC不是；

对于BD，，B是，D不是.

故选：B

第6题 (单选题) 难度 - ：

函数，的最小正周期为（）

A:
B:
C:
D:

解析:

找出的值，代入周期公式即可求出最小正周期．

，

，

，

则函数的最小正周期为．

故选：A．

第7题 (单选题) 难度 - ：

已知函数的图象关于直线对称，则的值为（）

A:
B:
C:
D:

解析:

由正弦函数的图象的对称性可得，由此可以求出的值.

由题得：，故，而，所以.

故选：B.

第8题 (单选题) 难度 - ：

函数的图象大致为（）

A:
B:
C:
D:

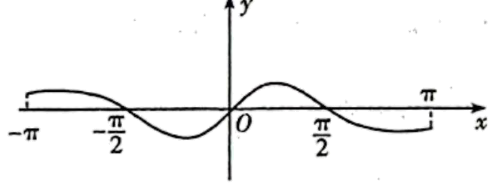
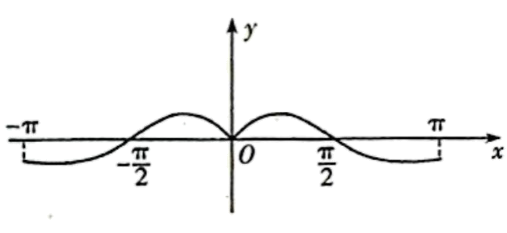
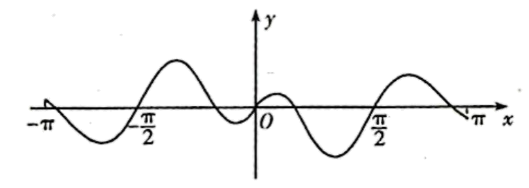
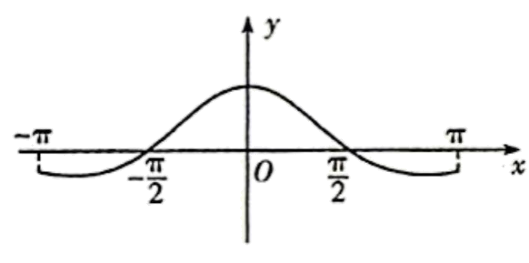
解析:

由函数的奇偶性判断排除B，D，再由时，，排除C，即可求解.

因为，所以函数为奇函数，故排除B，D，因为时，，则，故排除C.

故选：A

第9题 (单选题) 难度 - ：

在函数①，②，③，④中，最小正周期为π的函数有（　　）

A: ①③
B: ①④
C: ③④
D: ②③

解析:

根据函数图象的翻折变换和周期公式可得.

①由余弦函数的奇偶性可知，，最小值周期为；

②由翻折变换可知，函数的图象如图：

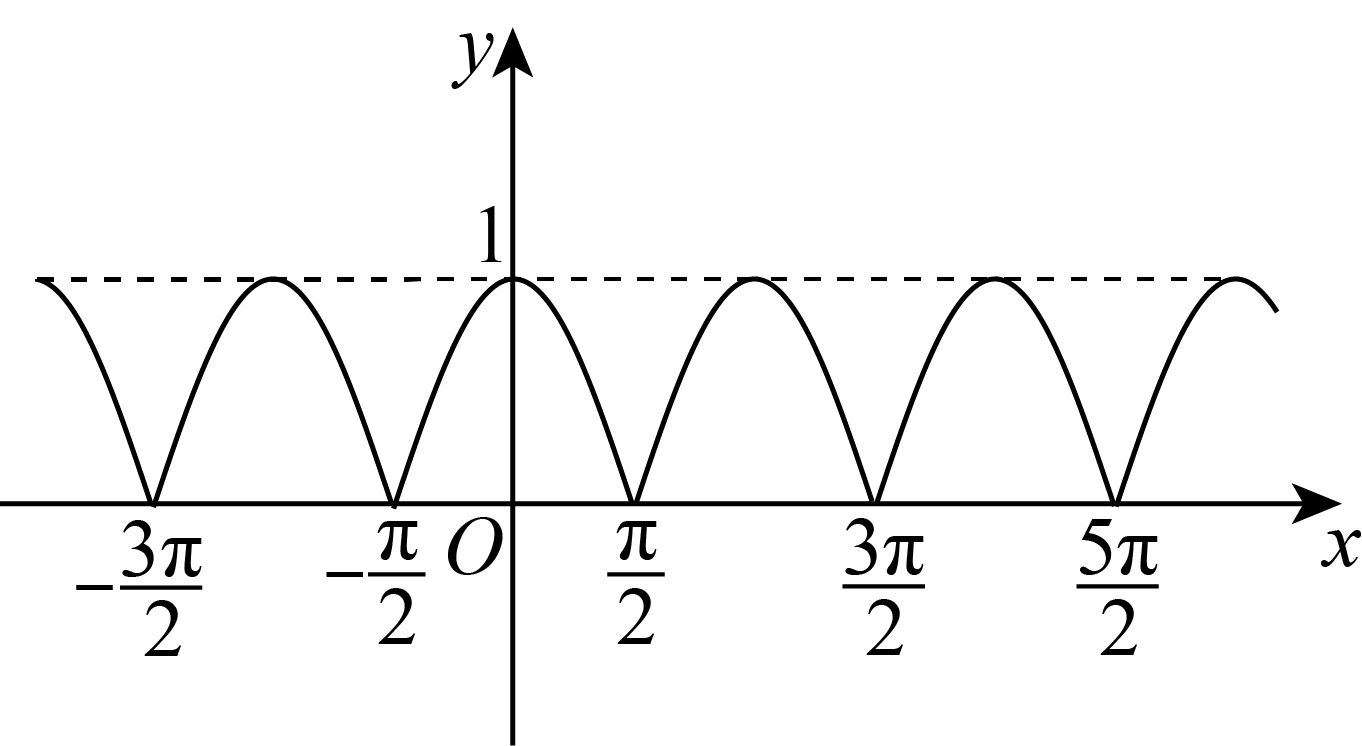
由图知的最小值周期为；

③由周期公式得，所以的最小值周期为；

④的最小值周期为.

故选：D

第10题 (单选题) 难度 - ：

设，，，则下列结论成立的是（）

A:
B:
C:
D:

解析:

将转化为，再结合正弦函数的增减性和函数值域，即可求解

，因时，为增函数，

故，又，故

故选：C

【点睛】本题考查由三角函数诱导公式和的增减性判断函数值的大小，属于基础题

第11题 (单选题) 难度 - ：

下列函数中是奇函数且最小正周期是π的函数是（）

A: y=cos|2x|
B: y=|sinx|
C: y=sin
D: y=cos

解析:

根据函数解析式判断奇偶性，结合最小正周期即可得出结果．

y=cos|2x|是偶函数，A错；

y=|sinx|是偶函数，B错；

y=sin=cos2x是偶函数，C错；

y=cos=-sin2x是奇函数，根据公式求得其最小正周期T=π，D正确．

故选：D

第12题 (单选题) 难度 - ：

已知函数的图象的相邻两条对称轴间的距离为，．则下列选项正确的是（）

A:
B: 的图象的对称轴方程为（）
C: 的单调递减区间为（）
D: 的解集为（）

解析:

由题意，求出函数的解析式，然后根据余弦型函数的图象与性质即可求解.

解：对A：因为函数的图象的相邻两条对称轴间的距离为，所以，故选项A错误；

对B：因为，所以，因为，所以，

所以，令（）得（），

即的图象的对称轴方程为（），故选项B错误；

对C：令（）得（），

即的单调递减区间为（），故选项C错误；

对D：令，得，

所以（），解得（），

所以的解集为（），故选项D正确．

故选：D．

第13题 (单选题) 难度 - ：

已知函数图象的相邻两条对称轴之间的距离为，且关于点对称，则的值为（）

A:
B:
C:
D:

解析:

根据对称轴的性质，结合正弦型函数的周期公式、对称性进行求解即可.

因为函数图象的相邻两条对称轴之间的距离为，

所以该函数的最小正周期为，

又因为，所以有，即，

因为该函数关于点对称，

所以，

因为，

所以令，

故选：B

第14题 (单选题) 难度 - ：

已知函数，设甲：，乙：是偶函数，则（）

A: 甲是乙的充分条件但不是必要条件
B: 甲是乙的必要条件但不是充分条件
C: 甲是乙的充要条件
D: 甲既不是乙的充分条件也不是乙的必要条件

解析:

根据正弦函数与余弦函数的奇偶性结合诱导公式即可判断.

当时，，为偶函数，甲是乙的充分条件；

若为偶函数，则，则反向无法推出，

所以甲是乙的充分条件但不是必要条件，

故选：A．

第15题 (单选题) 难度 - ：

已知在上有两个零点，则的取值范围为

A: （1，2）
B: [1，2]
C: [1,2)
D: （1，2]

解析:

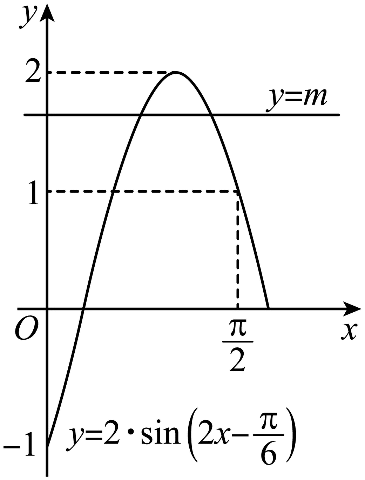
由题意在上有两个零点可转化为与在上有两个不同交点，作出如图的图象，

由于右端点的坐标是由图知，

故选C

【点睛】本题考查正弦函数的图象，解答本题关键是将函数有两个零点的问题转化为两个函数有两个交点的问题，作出两函数的图象，判断出参数的取值范围，本题以形助数，是解此类题常用的方法，熟练作出相应函数的图象对解答本题很重要

第16题 (多选题) 难度 - ：

下列关于函数的说法中正确的是（）

A: 最小正周期为
B: 最小正周期为
C: 为偶函数
D: 为奇函数

解析:

化简函数，再根据三角函数性质作答即可.

故最小正周期为，为奇函数

故选：AD

第17题 (多选题) 难度 - ：

下列不等式成立的是（）

A:
B:
C:
D:

解析:

结合正弦函数、余弦函数在各个区间的单调性判断.

因为，且函数在上单调递增，则，故选项A错误；

因为，且函数在上单调递减，则，即，故选项B正确；

因为，且函数在上单调递减，则，故选项C错误；

因为，且函数在上单调递减，则，故选项D正确；

故选：BD

第18题 (多选题) 难度 - ：

（多选）设函数，，则关于的说法正确的是（）

A: 最小正周期为
B: 最小正周期为
C: 奇函数
D: 偶函数

解析:

正弦型函数的周期可代入公式去求，奇偶性的判断，可以使用诱导公式看是否能转化为或形式来判定.

，最小正周期,排除B，选A;

由

可知函数为偶函数，排除C，选D

故选:AD.

第19题 (多选题) 难度 - ：

下列坐标所表示的点是函数图象的对称中心的是（）

A:
B:
C:
D:

解析:

利用正切函数的性质即可求解.

由已知，令，得．

当时，，所以函数图象的对称中心的是，所以D正确；

当时，，所以函数图象的对称中心的是，所以B正确；

当时，，所以函数图象的对称中心的是，所以A正确；

显然选项C错误.

故选：ABD．

第20题 (多选题) 难度 - ：

(多选)函数是R上的偶函数，则的值可以是（）

A:
B:
C:
D:

解析:

利用函数奇偶性的性质可得，进而可得答案.

因为函数为上的偶函数，

函数的图象关于轴对称，

可得，

则，；

所以时，

的值分别是，

故选：ACD．

第21题 (多选题) 难度 - ：

下列函数中最小正周期为的是（）

A:
B:
C:
D:

解析:

根据周期公式计算可知、正确；不正确；根据的图象可知正确.

对于，，故正确；

对于，，故正确；

对于，，故不正确；

对于，因为的图象是由的图象进行翻折变换得到的，所以的最小正周期为.故正确.

故选：ABD

【点睛】关键点点睛：根据的图象求最小正周期是本题解题关键.

第22题 (多选题) 难度 - ：

已知函数，则下列命题中正确的有（）

A: 的最小正周期为
B: 的定义域为
C: 图象的对称中心为，
D: 的单调递增区间为，

解析:

根据正切函数的图象及性质解决即可.

由题知，函数，

所以的最小正周期为，故A正确；

的定义域满足，即

所以的定义域为，故B错误；

图象的对称中心应满足，即，

所以图象的对称中心为，，故C正确；

的单调递增区间应满足，即，,

所以的单调递增区间为，，故D正确；

故选：ACD

第23题 (多选题) 难度 - ：

函数在下列区间上单调递增的是（）

A:
B:
C:
D:

解析:

根据题意求出函数的单调递增区间，进而判断答案.

，由，，解得，.当时，有；当时，有，只有B,C符合.

故选：BC.

第24题 (多选题) 难度 - ：

已知函数，则说法正确的是（）

A: 的图象关于点对称
B: 的图象关于直线对称
C: 为奇函数
D: 为偶函数

解析:

根据三角函数的图象和性质以及奇偶函数的定义即可得答案.

对于A选项，因为，

所以，

的图象关于点对称，所以A选项正确.

对于B选项，由，

知的图象不关于直线对称，所以B选项错误.

对于C选项，由，

知为奇函数，所以C选项正确.

对于D选项，因为，

，

，所以不为偶函数，所以D选项错误.

故选:AC.

第25题 (多选题) 难度 - ：

下列结论正确的是（）

A: 的最小正周期是
B: 若圆心角为的扇形的弧长为，则该扇形面积为
C: 若角的终边过点，则
D: 若角为锐角，则角为钝角

解析:

对于选项A：利用的最小正周期为计算即可.

对于选项B：利用公式即可计算出答案.

对于选项C：利用，即可计算出答案.

对于选项D：当时，为直角.则可判断出答案.

的周期是；A错误.

若圆心角为的扇形的弧长为，则该扇形的半径为，该扇形面积为;B正确.

若角的终边过点，则.C正确.

当时，为直角.D错误.

故选：BC.

第26题 (多选题) 难度 - ：

已知函数，则（）

A: 是偶函数
B: 在区间单调递增
C: 的图像关于点对称
D: 的图像关于直线对称

解析:

对于A：先化简，再借助于为偶函数进行判断；对于B：利用复合函数的单调性法则直接判断；对于C、D：利用代入法进行判断.

对于A：.

因为为偶函数，所以为偶函数.故A正确；

对于B：当时，.

因为在上递增，在上单减，所以在区间不单调.故B错误；

对于C：因为，所以的图像关于点对称.故C正确；

对于D：因为，所以的图像关于直线对称.故D正确；

故选：ACD.

第27题 (多选题) 难度 - ：

下列说法正确的是（）

A: 函数的最小正周期为
B: 函数的定义域是
C:
D: 若一扇形弧长为，圆心角为，则该扇形的面积为

解析:

根据余弦型函数最小正周期求法可知A正确；根据正切型函数定义域的求法可知B错误；利用同角三角函数关系和诱导公式可求得C正确；根据扇形弧长和面积公式可求得D正确.

对于A，的最小正周期，A正确；

对于B，令，解得：，

的定义域为，B错误；

对于C，，C正确；

对于D，设扇形半径为，则，解得：，

扇形面积，D正确.

故选：ACD.

第28题 (解答题) - 简答题难度 - ：

已知函数．

(1)写出的最小正周期；

(2)求的最小值，并求取得最小值时自变量的集合．

答案:

(1)

(2)最小值为，自变量的集合为

解析:

（1）利用求周期的公式求解；

（2）利用正弦型函数的性质可求最值及自变量的集合.

（1）∵函数，

∴的最小正周期为．

（2）对于函数，

当，时，即当时，时，取得最小值为．

所以函数取得最小值时自变量的集合为．

第29题 (解答题) - 简答题难度 - ：

已知函数.

(1)求的单调递增区间；

(2)求在上的值域.

答案:

(1)

(2)

解析:

（1）根据余弦函数的性质计算可得.

（2）由的取值范围求出，再根据余弦函数的性质计算可得.

（1），令，

解得，

所以函数的单调递增区间为.

（2），因为，所以，

可得，则，

即函数在上的值域为．

第30题 (解答题) - 简答题难度 - ：

已知函数.

(1)求函数图像的对称中心；

(2)求函数图像的单调递减区间.

答案:

(1)

(2)

解析:

（1）根据余弦函数的性质求对称中心；

（2）根据余弦函数的性质求单调递减区间.

（1）令，解得，

所以函数图像的对称中心为.

（2）令，

解得，

所以函数图像的单调递减区间为.

第31题 (解答题) - 简答题难度 - ：

已知函数．

(1)求的单调递增区间；

(2)求在区间上的值域.

答案:

(1)

(2)

解析:

（1）解不等式可得出函数的单调递增区间；

（2）由可求得的取值范围，由正弦函数的基本性质可求得函数的值域.

（1）由可得，

所以，函数的单调递增区间为.

（2）当时，，则，

所以，.

因此，函数在区间上的值域为.