如图,终边在阴影部分(含边界)的角的集合是 .
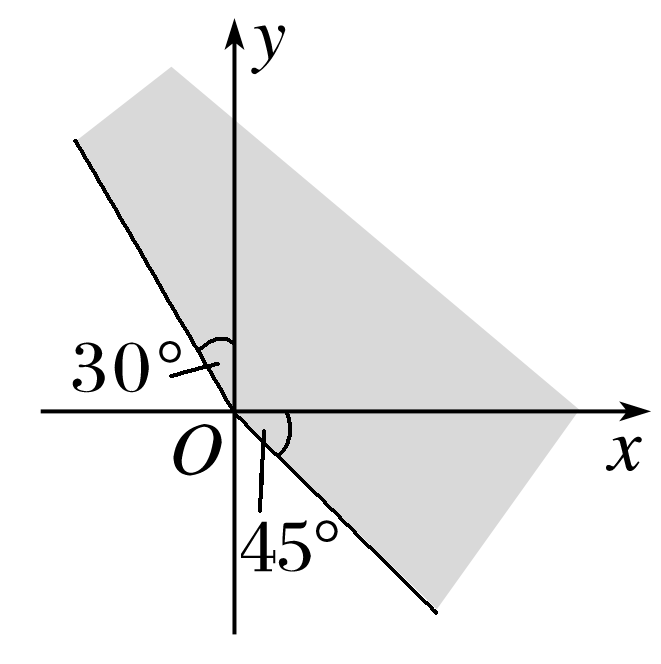
答案: {α|-45°+k·360°≤α≤120°+k·360°,k∈Z}
3 888°的终边落在( )
解析:
因为3 888°=288°+10×360°,
又因为288°的终边落在第四象限,
所以3 888°的终边落在第四象限.
下面各组角中,终边相同的是( )
解析:
因为-330°=-360°+30°,750°=2×360°+30°,
所以-330°与750°终边相同.
(课本P175习题5.1 T7(2))已知α为锐角,则2α为( )
解析:
因为α为锐角,所以0°<α<90°,
则0°<2α<180°.
时针走过2小时40分,则分针转过的角度是( )
解析:
40÷60=,360°×=240°.
∵时针、分针都是顺时针旋转,
∴时针走过2小时40分,分针转过的角度为-2×360°-240°=-960°.
角α的终边与65°角的终边关于y轴对称,则α等于( )
解析:
因为大小为115°的角的终边与大小为65°的角的终边关于y轴对称,所以α=k·360°+115°(k∈Z).
(多选)下列四个角中,属于第二象限角的是( )
解析:
A中,160°很显然是第二象限角;
B中,480°=120°+360°,是第二象限角;
C中,-960°=-3×360°+120°,是第二象限角;
D中,1 530°=4×360°+90°,不是第二象限角.
(多选)下列说法中,正确的是( )
解析:
终边落在第一象限的角不一定是锐角,如400°的角是第一象限角,但不是锐角,故A说法错误;同理第二象限角也不一定是钝角,故C说法错误;BD正确.
(多选)下列角的终边与37°角的终边在同一直线上的是( )
解析:
与37°角的终边在同一直线上的角可表示为37°+k·180°,k∈Z.
当k=10时,37°+1 800°=1 837°;当k=-2时,37°-360°=-323°;当k=-5时,37°-900°=-863°.
已知角α=-130°,则角α的终边落在第 象限.
答案: 三
解析:
因为-180°<-130°<-90°,所以角α的终边落在第三象限.
与-457°角终边相同的角的集合是 .
答案: {α|α=263°+k·360°,k∈Z}
解析:
由于-457°=-2×360°+263°,故与-457°角终边相同的角的集合是{α|α=263°+k·360°,k∈Z}.
终边落在x轴非正半轴上的角α的集合为 .
答案: {x|x=2kπ+π,k∈Z}
解析:
根据终边相同角的表示方法,可得终边落在x轴非正半轴上的角α的集合为{x|x=2kπ+π,k∈Z}.
如图,终边在阴影部分(含边界)的角的集合是 .

答案: {α|-45°+k·360°≤α≤120°+k·360°,k∈Z}
已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
答案: 解 (1)α=-1 910°=-6×360°+250°,它是第三象限角. (2)令θ=250°+n·360°(n∈Z), 取n=-1,-2就得到符合-720°≤θ<0°的角. 当n=-1时,θ=250°-360°=-110°; 当n=-2时,θ=250°-720°=-470°. 故θ=-110°或θ=-470°.
已知角β以坐标原点O为顶点,以x轴非负半轴为始边,终边落在x轴绕点O逆时针旋转60°所得的直线上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
答案: 解 (1)由题可知,角β的集合S={β|β=60°+k·180°,k∈Z}. (2)在S={β|β=60°+k·180°,k∈Z}中, 取k=-2,得β=-300°;取k=-1,得β=-120°; 取k=0,得β=60°;取k=1,得β=240°; 取k=2,得β=420°;取k=3,得β=600°. 所以S中适合不等式-360°<β<720°的元素分别是-300°,-120°,60°,240°,420°,600°.
写出角α的终边在下列位置时的集合S.
(1)角α的终边在如图(1)所示的阴影中(包括边界);
(2)角α的终边在如图(2)所示的阴影中(包括边界).
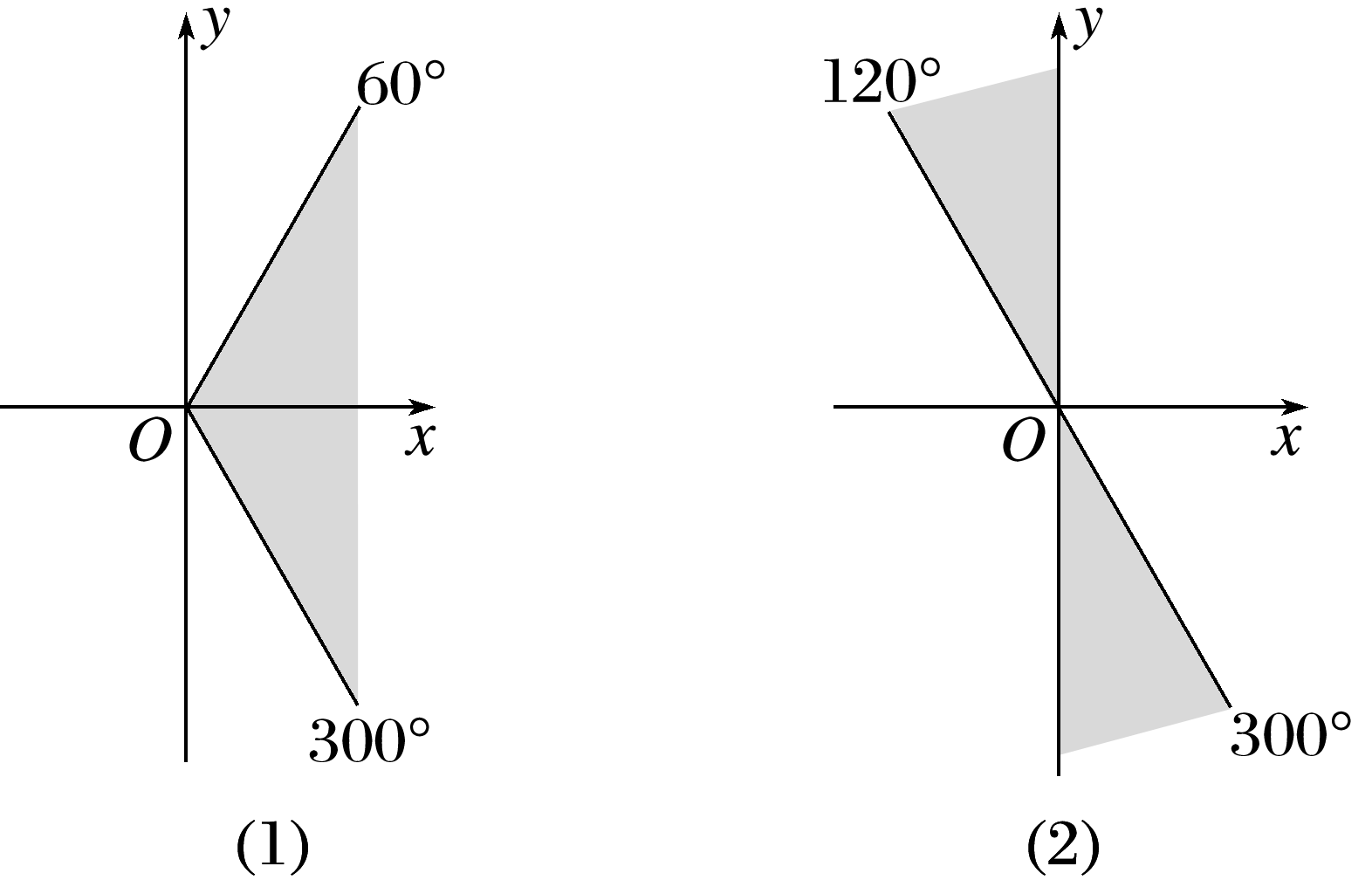
答案: 解 (1)由题意知,角α的集合为S={α|-60°+k·360°≤α≤60°+k·360°,k∈Z}. (2)由题意知,角α的集合为S={α|k·360°+90°≤α≤k·360°+120°,k∈Z}∪{α|k·360°+270°≤α≤k·360°+300°,k∈Z}={α|k·180°+90°≤α≤k·180°+120°,k∈Z}.
在平面直角坐标系中,用阴影表示下列集合:
(1){α|30°+k·360°≤α≤60°+k·360°,k∈Z};
(2){α|30°+k·180°≤α≤60°+k·180°,k∈Z}.
答案: 解 (1) 根据任意角的定义,画出集合{α|30°+k·360°≤α≤60°+k·360°,k∈Z}对应的区域,如图1中阴影部分(含边界)所示. (2)根据任意角的定义,画出集合{α|30°+k·180°≤α≤60°+k·180°,k∈Z}对应的区域,如图2中阴影部分(含边界)所示.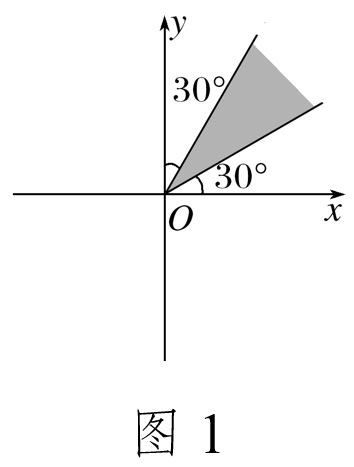
若α是第一象限角,则-是( )
解析:
由题意知,k·360°<α<k·360°+90°,k∈Z,
则k·180°<<k·180°+45°,所以-k·180°-45°<-<-k·180°,k∈Z,
当k为偶数时,-为第四象限角;当k为奇数时,-为第二象限角,
所以-是第二或第四象限角.
已知角α的集合为{α|α=45°+k·90°,k∈Z}.
(1)在角α的集合中有几种终边不相同的角?
(2)在角α的集合中,有几个大于-360°且小于360°的角?
答案: 解 (1)由k=4n,4n+1,4n+2,4n+3(n∈Z),知在角α的集合中终边不相同的角共有四种. (2)由-360°<45°+k·90°<360°,得-<k<. 又k∈Z,故k=-4,-3,-2,-1,0,1,2,3. 所以在角α的集合中,大于-360°且小于360°的角共有8个.