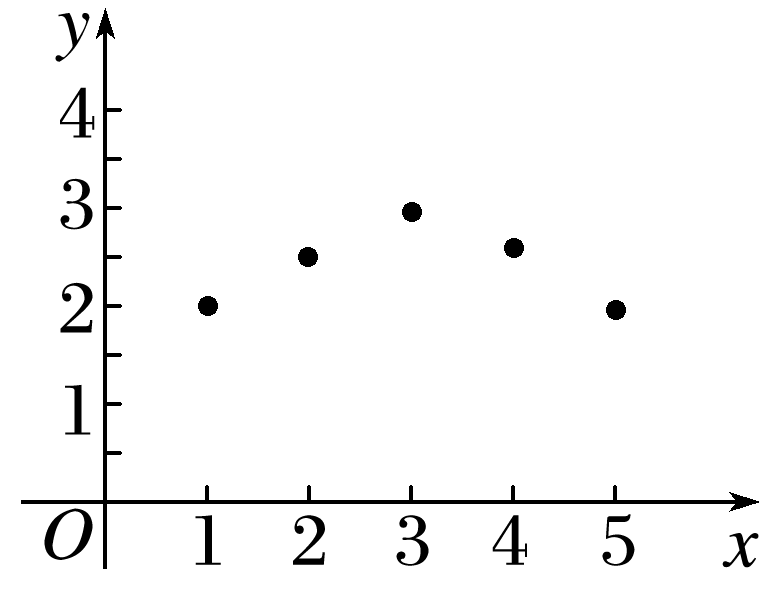
某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可选择的模拟函数模型是( )
- A: y=ax+b
- B: y=ax2+bx+c
- C: y=aex+b
- D: y=aln x+b
解析:
从所给的散点图可看出函数的变化趋势是先增后减,所以该函数模型是二次函数.
(课本P160复习参考题4 T5(1))已知集合A={y|y=log2x,x>1},B=,则A∩B等于( )
解析:
A={y|y=log2x,x>1}={y|y>0},B==,所以A∩B=.
函数f(x)=2ax-1-1(a>0,且a≠1)恒过定点( )
解析:
由题意知,x-1=0,即x=1,
此时f(x)=2a0-1=1,
所以函数恒过定点(1,1).
下列四个函数中,在(0,+∞)上单调递减的是( )
解析:
y=在(0,+∞)上单调递增,故A错误;
y=-x2+x=-+,在上单调递增,在上单调递减,故B错误;
y=2x在(0,+∞)上单调递增,故C错误;
y=log2x在(0,+∞)上单调递增,故y=-log2x在(0,+∞)上单调递减,故D正确.
某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可选择的模拟函数模型是( )

解析:
从所给的散点图可看出函数的变化趋势是先增后减,所以该函数模型是二次函数.
函数f(x)=+lg (5-3x)的定义域是( )
解析:
由得即1≤x<.
设f(x)=3x-x2,则在下列区间中,使函数f(x)有零点的区间是( )
解析:
∵f(-1)=3-1-(-1)2=-1=-<0,
f(0)=30-02=1>0,
∴f(-1)f(0)<0,
∴使函数f(x)有零点的区间是[-1,0].
设a=20.7,b=,c=log60.7,则( )
解析:
因为c=log60.7<0<b=<1<a=20.7,
所以c<b<a.
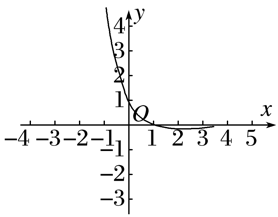
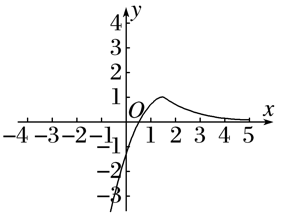
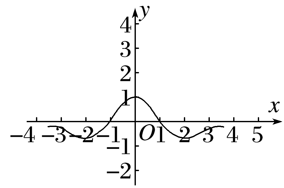
函数f(x)=的图象大致为( )
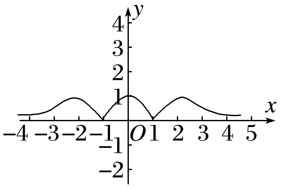
解析:
当x<1时,1-x>0,f(x)=>0,故排除B,C;
当x>1时,1-x<0,f(x)=<0,故排除D.
(多选)下列计算成立的是( )
解析:
log28-log24=log2=log22=1,故A选项错误;
log35+log34=log3(5×4)=log320,故B选项错误;
lg 2+lg 5=lg (2×5)=lg 10=1,故C选项正确;
log223=3log22=3,故D选项正确.
(多选)若直线y=3a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,则a可以是( )
解析:
由题意,直线y=3a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,
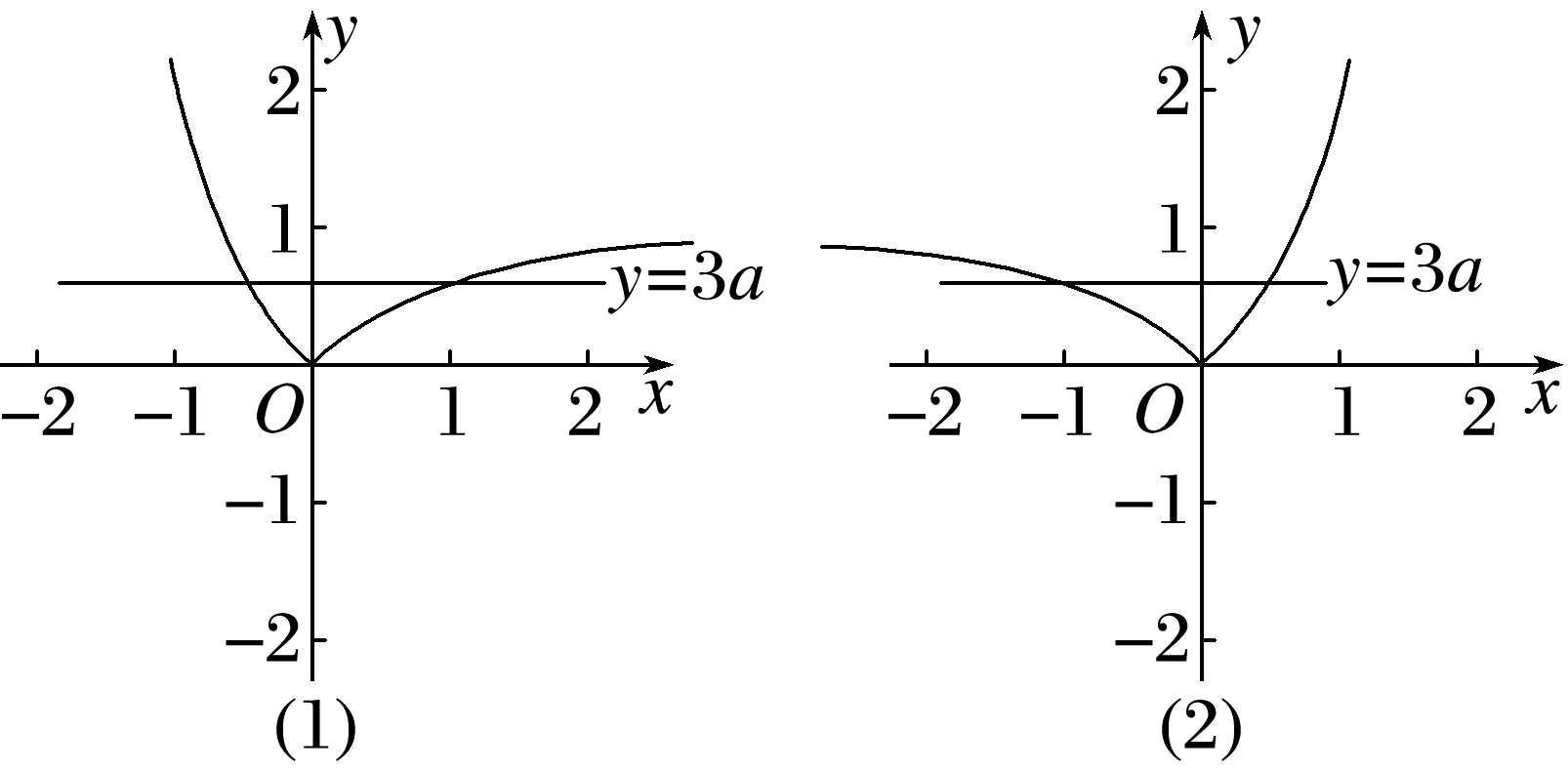
当0<a<1时,y=|ax-1|的图象如图(1)所示,
由已知得0<3a<1,∴0<a<;
当a>1时,y=|ax-1|的图象如图(2)所示,
由已知可得0<3a<1,
∴0<a<,结合a>1可得a无解.
综上可知,a的取值范围为.
(多选)边际函数是经济学中的一个基本概念,在国防、医学、环保和经济管理等许多领域中都有十分广泛的应用,函数f(x)的边际函数Mf(x)定义为Mf(x)=f-f(x).某公司每月最多生产75台报警系统装置,生产x台的收入函数R(x)=3000x-20x2(单位:元),其成本函数C(x)=500x+4000(单位:元),利润是收入与成本之差,设利润函数为P(x),则以下说法正确的是( )
解析:
对于A选项,P(x)=R(x)-C(x)=-20x2+2500x-4000,二次函数P(x)的图象开口向下,对称轴为直线x==62.5,因为x∈N*,所以P(x)取得最大值时,每月产量为63台或62台,A错;对于B选项,MP(x)=P-P(x)=-20+2500-4000-=2480-40x,B对;对于C选项,P(x)max=P=P=74120,因为函数MP(x)=2480-40x为减函数,则MP(x)max=MP=2440,C对;对于D选项,函数MP(x)=2480-40x为减函数,说明随着产量的增加,每台利润与前一台利润差额在减少,D对.
lo5-lo45+的值为 .
答案: 10
解析:
原式=lo+=lo+23=2+8=10.
用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:

据此数据,可得方程3x-x-4=0的一个近似解(精确度为0.01)可取 .
答案: 1.5562(答案不唯一)
解析:
由f(1.5625)f(1.5562)<0,且|1.5562-1.5625|=0.0063<0.01,得方程3x-x-4=0的一个近似解可以为1.5562.
已知函数f(x)=若关于x的方程f(x)-m=0恰有两个不同的实数解,则实数m的取值范围为 .
答案: [1,3)∪{0}
解析:
因为关于x的方程f(x)-m=0恰有两个不同的实数解,
所以函数y=f(x)的图象与直线y=m有两个交点,作出函数图象,如图所示,
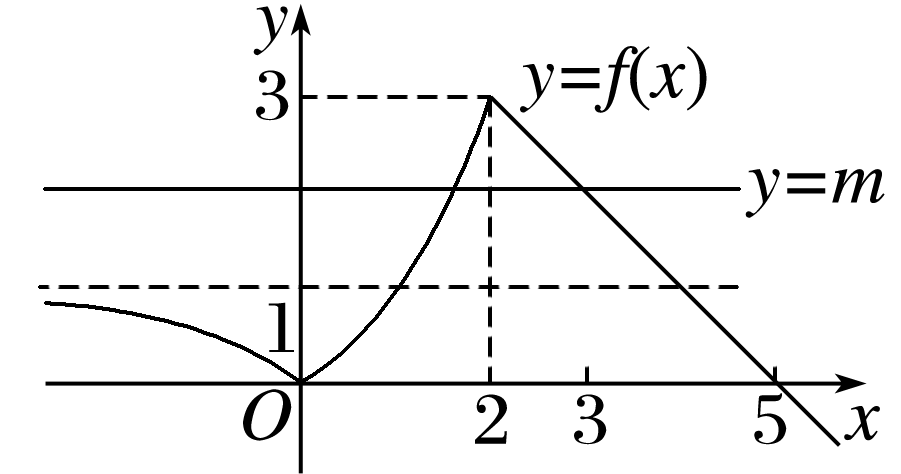
所以当m∈[1,3)∪{0}时,函数y=f(x)的图象与直线y=m有两个交点,
所以实数m的取值范围是[1,3)∪{0}.
(1)计算:lg +2lg 2+log25×log54;
(2)求不等式<52x+2的解集.
答案: 解 (1)lg +2lg 2+log25×log54=lg +lg 22+log25×log522 =lg +2log25×log52=lg 10+2=1+2=3. (2)<52x+2, 即(5-1<52x+2,即<52x+2, 因为函数y=5x在R上是增函数, 所以x2-1<2x+2,即x2-2x-3<0, 解得-1<x<3, 所以原不等式的解集为(-1,3).
已知函数f(x)=4x+m·4-x.
(1)若f(x)为偶函数,求实数m的值;
(2)若f(x)为奇函数,求实数m的值;
答案: 解 (1)若f(x)为偶函数, 则f(-x)=4-x+m·4x=f(x)=4x+m·4-x, 即(m-1)(4x-4-x)=0, 则m-1=0,解得m=1. (2)若f(x)为奇函数, 则f(-x)=4-x+m·4x=-f(x)=-4x-m·4-x, 即(m+1)(4x+4-x)=0, 则m+1=0,解得m=-1.
已知函数y=log4(2x+3-x2).
(1)求函数的定义域;
(2)求y的最大值,并求取得最大值时的x值.
答案: 解 (1)由真数2x+3-x2>0, 解得-1<x<3, 所以函数的定义域为{x|-1<x<3}. (2)将原函数分解为y=log4u,u=2x+3-x2两个函数. 因为u=2x+3-x2=-(x-1)2+4≤4, 所以当x=1时,u取得最大值4, 又y=log4u为增函数, 所以y=log4(2x+3-x2)≤log44=1. 所以y的最大值为1, 此时x=1.
已知指数函数f(x)=ax(a>0,且a≠1)过点(m,n),在①+=0;②函数y=x2-2x+4的顶点坐标为(m,n);③函数y=logbx+3(b>0,且b≠1)过定点(m,n)这三个条件中任选一个,回答下列问题.
(1)求f(x)的解析式,并判断g(x)=f(x)+的奇偶性;
(2)解不等式:loga(1+x)<loga(2-x).
注:如果选择多个条件分别解答,则按第一个解答计分.
答案: 解 (1)由①可知,+=0, 即解得 由②可知,函数y=x2-2x+4=(x-1)2+3的顶点坐标为(1,3), 则 由③可知,函数y=logbx+3(b>0,且b≠1)过定点(1,3), 则 综上,三个条件中任选一个, 均有即f(x)=ax过点(1,3), 即a=3,f(x)=3x. g(x)=f(x)+=3x+3-x,x∈R, g(-x)=f(-x)+=3-x+3x=g(x), ∴g(x)为偶函数. (2)loga(1+x)<loga(2-x), 即log3(1+x)<log3(2-x), 可化为2-x>1+x>0, ∴-1<x<. 即不等式loga(1+x)<loga(2-x)的解集为.
某化工厂每一天中污水污染指数f(x)与时刻x(时)的函数关系为f(x)=|log25(x+1)-a|+2a+1,x∈[0,24],其中a为污水治理调节参数,且a∈(0,1).
(1)若a=,求一天中哪个时刻污水污染指数最低;
(2)规定每天中f(x)的最大值作为当天的污水污染指数,要使该厂每天的污水污染指数不超过3,则调节参数a应控制在什么范围内?
答案: 解 (1)因为a=, 则f(x)=+2≥2. 当f(x)=2时,log25(x+1)-=0, 得x+1=2=5,即x=4. 所以一天中早上4点该厂的污水污染指数最低. (2)设t=log25(x+1), 则当0≤x≤24时,0≤t≤1. 设g(t)=|t-a|+2a+1,t∈[0,1], 则g(t)= 显然g(t)在[0,a]上单调递减,在(a,1]上单调递增, 则f(x)max=max{g(0),g(1)}, 因为g(0)=3a+1,g(1)=a+2, 则有 解得a≤, 又a∈(0,1), 故调节参数a应控制在内.