函数f(x)=的图象大致为( )
- A:
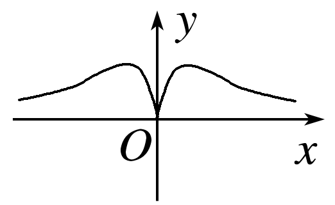
- B:
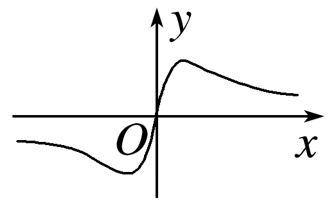
- C:
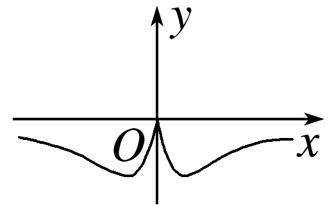
- D:
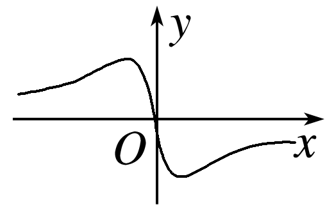
解析:
f(x)的定义域为R,
∵f(-x)===f(x),
∴f(x)为偶函数,排除B,D,
又∵f(x)≥0,故选A.
设函数f(x)=若f(x)是奇函数,则g(-2)等于( )
解析:
由已知可得g(-2)=f(-2)=-f(2)=-(22-2×2)=0.
已知函数f(x)是R上的奇函数,且在区间[0,+∞)上单调递减,则下列结论正确的是( )
解析:
因为f(x)是R上的奇函数,且在区间[0,+∞)上单调递减,
则f(x)在(-∞,0]上也单调递减,
所以f(x)在R上单调递减,
因为-1<0<2,
所以f(2)<f(0)<f(-1).
如果奇函数f(x)在区间[-3,-1]上单调递增且有最大值5,那么函数f(x)在区间[1,3]上( )
解析:
∵f(x)为奇函数,
∴f(x)在[1,3]上的单调性与在[-3,-1]上一致,
∴f(x)在区间[1,3]上单调递增,
又f(x)在区间[-3,-1]上有最大值5,
∴f(x)在区间[1,3]上有最小值-5.
函数f(x)=的图象大致为( )




解析:
f(x)的定义域为R,
∵f(-x)===f(x),
∴f(x)为偶函数,排除B,D,
又∵f(x)≥0,故选A.
函数y=f(x)是R上的偶函数,且在[0,+∞)上单调递减,若f(m)≤f(4),则实数m的取值范围是( )
解析:
由题意,偶函数y=f(x)在(-∞,0)上单调递增,在[0,+∞)上单调递减,
又f(m)≤f(4),则|m|≥4⇒m≤-4或m≥4.
(多选)一个偶函数定义在区间[-7,7]上,它在[0,7]上的图象如图所示,下列说法正确的是( )
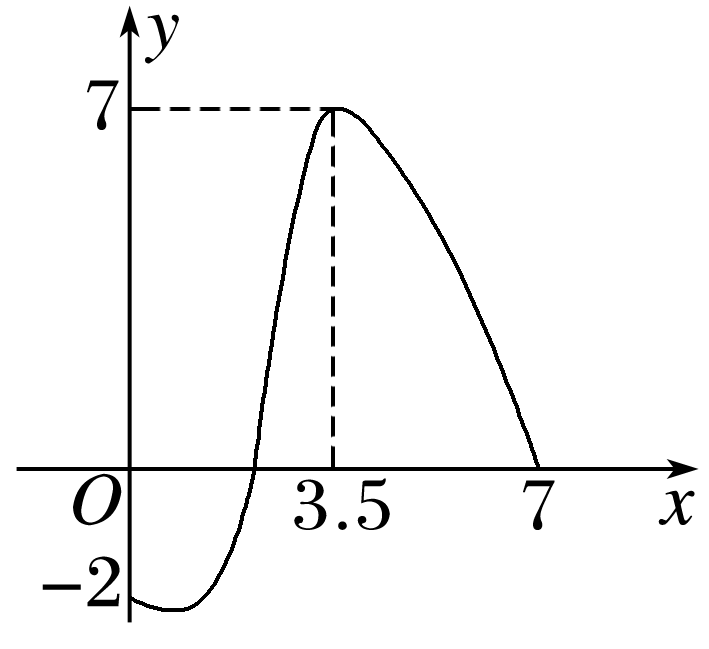
解析:
根据偶函数在[0,7]上的图象及其对称性,作出函数在[-7,0]上的图象,如图所示,
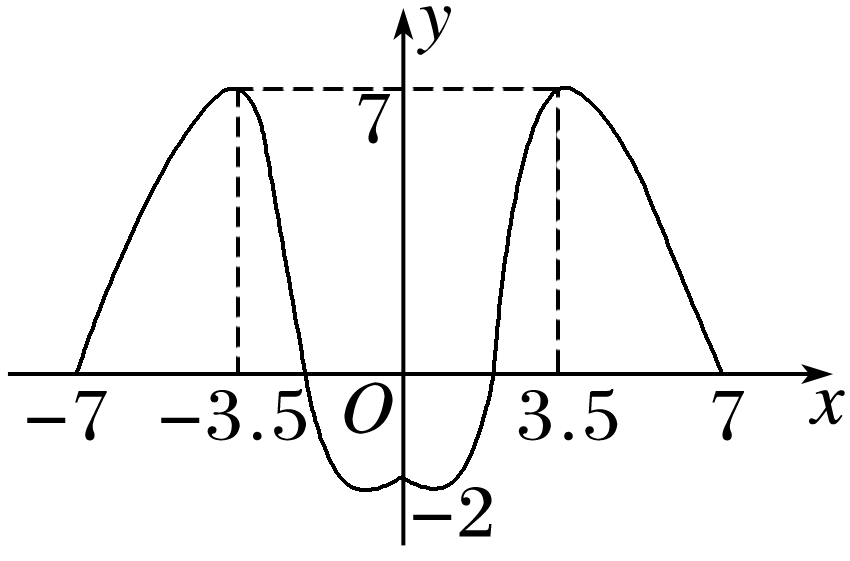
可知这个函数有三个单调递增区间,有三个单调递减区间,在其定义域内有最大值7,在其定义域内的最小值不是-7.
(多选)已知函数f(x)是偶函数,且在区间[0,5]上单调.若f(-4)<f(-2),则下列不等式不成立的是( )
解析:
由题意可得,函数f(x)在区间[-5,0]上也单调,再根据f(-4)<f(-2),可得函数f(x)在区间[-5,0]上单调递增,所以函数f(x)在区间[0,5]上单调递减,故f(-1)=f(1)>f(3),f(2)>f(3),f(-3)=f(3)>f(5),f(0)>f(1).
(多选)函数f(x)的图象是折线段ABC,如图所示,其中点A,B,C的坐标分别为(-1,2),(1,0),(3,2),以下说法正确的是( )
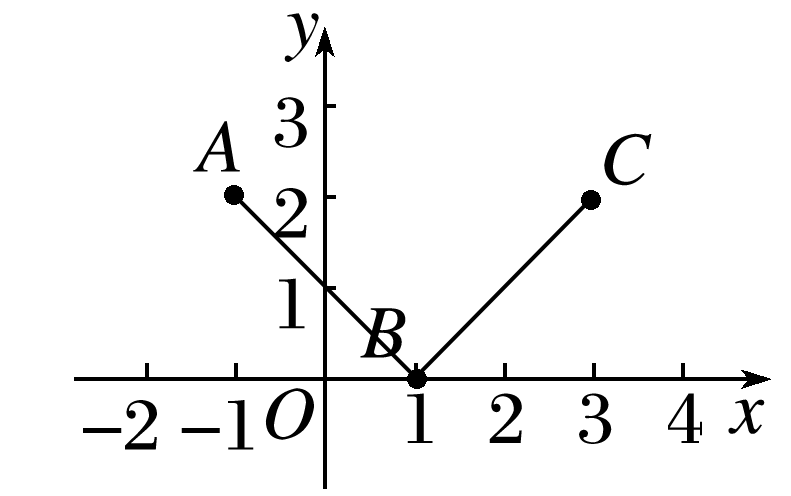
解析:
因为点A,B,C的坐标分别为(-1,2),(1,0),(3,2),
所以f(x)=
故A正确;
因为f(x)的定义域为[-1,3],所以f(x-1)的定义域为[0,4],故B错误;
因为f(x)的图象向左平移1个单位长度后关于y轴对称,所以f(x+1)为偶函数,故C正确;
由图象可知m的最小值为1,故D正确.
设偶函数f(x)在区间(-∞,-2)上单调递减,则f(3)与f(-4)的大小关系为 .
答案: f(3)<f(-4)
解析:
∵f(x)为偶函数,∴f(-x)=f(x),
∴f(3)=f(-3),
又f(x)在区间(-∞,-2)上单调递减,
且-4<-3<-2,
∴f(3)=f(-3)<f(-4).
已知函数f(x)是定义在[-3,3]上的奇函数,当x>0时,f(x)=-x(x+1).则函数f(x)的解析式为 .
答案: f(x)=
解析:
设-3≤x<0,则3≥-x>0,
则有f(-x)=x(-x+1)=-x(x-1),
又因为f(x)=-f(-x),
所以f(x)=x(x-1),又f(0)=0,
所以f(x)=
若f(x)=(m-1)x2+6mx+2是偶函数,则f(0),f(1),f(-2)从小到大的排列是 .
答案: f(-2)<f(1)<f(0)
解析:
∵f(x)是偶函数,∴f(-x)=f(x)恒成立,
即(m-1)x2-6mx+2=(m-1)x2+6mx+2恒成立,
∴m=0,即f(x)=-x2+2.
∵f(x)的图象开口向下,对称轴为y轴,在[0,+∞)上单调递减,
又2>1>0,∴f(2)<f(1)<f(0),
即f(-2)<f(1)<f(0).
已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若f(-3)=0,则<0的解集为 .
答案: {x|-3<x<0或x>3}
解析:
∵f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增,
∴f(x)在区间(0,+∞)上单调递减.
∴f(3)=f(-3)=0.
当x>0时,由f(x)<0,解得x>3;
当x<0时,由f(x)>0,
解得-3<x<0.
故所求解集为{x|-3<x<0或x>3}.
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x+-4.求函数f(x)在R上的解析式.
答案: 解 因为函数f(x)是定义在R上的奇函数, 所以f(0)=0,设x<0,则-x>0, 当x>0时,由f(x)=x+-4可知, f(-x)=-x--4, 又f(x)为奇函数, 故f(x)=-f(-x)=x++4(x<0), 所以函数f(x)在R上的解析式为 f(x)=
已知f(x)是定义在(-1,1)上的奇函数,且f(x)在(-1,1)上是减函数,解不等式f(1-x)+f(1-2x)<0.
答案: 解 ∵f(x)是定义在(-1,1)上的奇函数, 由f(1-x)+f(1-2x)<0,得 f(1-x)<-f(1-2x),即f(1-x)<f(2x-1). 又∵f(x)在(-1,1)上是减函数, ∴解得0<x<, ∴原不等式的解集为.
(课本P86习题3.2T11)已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.
答案: 解 因为f(x)是R上的奇函数, 所以f(-x)=-f(x). 因为当x≥0时,f(x)=x(1+x), 所以当x<0时,-x>0, 所以f(-x)=(-x)(1-x)=-x(1-x), 所以f(x)=-f(-x)=x(1-x). 所以f(x)= 它的图象如图所示.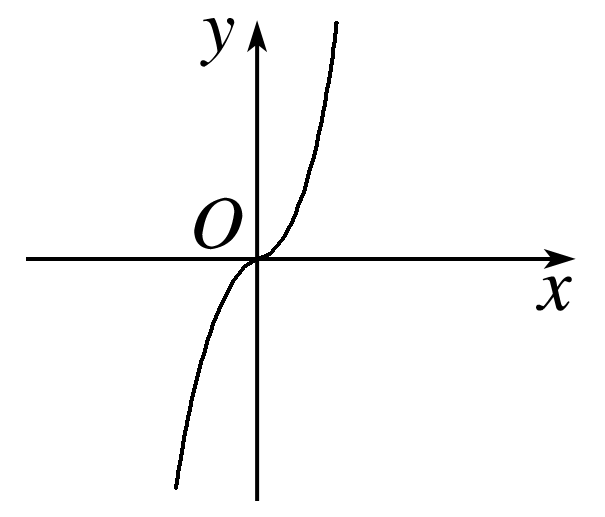
已知定义在R上的偶函数f(x),当x≥0时,f(x)=x2+2x.
(1)比较f(-2)与f(1)的大小;
(2)解不等式f(3x-2)<8.
答案: 解 (1)因为f(x)是偶函数,且当x≥0时,f(x)=x2+2x, 所以f(1)=12+2=3,f(-2)=f(2)=8, 所以f(-2)>f(1). (2)当x∈[0,+∞)时,令f(x)=x2+2x=8, 解得x1=2,x2=-4(舍去),即f(2)=8, 所以不等式f(3x-2)<8,即f(3x-2)<f(2), 又f(x)在R上为偶函数,f(x)在[0,+∞)上单调递增, 则|3x-2|<2,所以0<x<, 所以不等式的解集为.
已知定义在R上的奇函数满足f(x+8)=f(x),且在区间[0,2]上单调递增,则( )
解析:
∵f(x+8)=f(x),∴f(25)=f(17)=f(9)=f(1),同理f(80)=f(0),
又∵奇函数f(x)在区间[0,2]上单调递增,
∴f(x)在区间[-2,2]上单调递增,
∴f(-1)<f(0)<f(1),
即f(-1)<f(80)<f(25).
已知y=f(x)是奇函数,它在(0,+∞)上单调递增,且f(x)<0,试问F(x)=在(-∞,0)上单调递增还是单调递减?证明你的结论.
答案: 解 F(x)在(-∞,0)上单调递减. 证明如下:任取x1,x2∈(-∞,0),且x1<x2, 则有-x1>-x2>0. 因为y=f(x)在(0,+∞)上单调递增,且f(x)<0, 所以f(-x2)<f(-x1)<0, ① 又因为f(x)是奇函数, 所以f(-x2)=-f(x2),f(-x1)=-f(x1), ② 由①②得f(x2)>f(x1)>0. 于是F(x1)-F(x2)=>0, 即F(x1)>F(x2), 所以F(x)=在(-∞,0)上单调递减.