已知关于x的不等式ax2-x+c>0的解集为{x|-2<x<1},则函数y=ax2+x+c的图象为( )
- A:
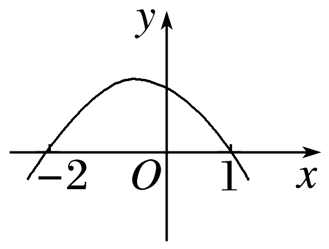
- B:
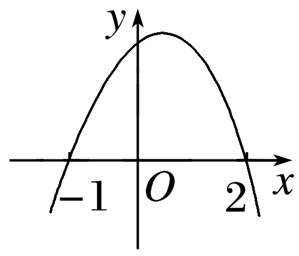
- C:
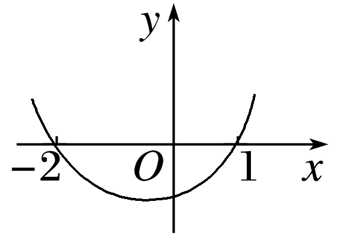
- D:
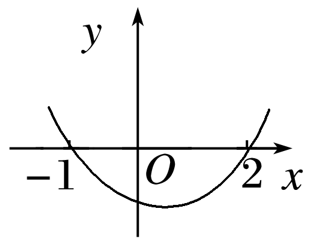
解析:
由题意可知,a<0且
∴
∴函数y=ax2+x+c=-x2+x+2的图象为B项.
下列命题中正确的是( )
解析:
∵ab>0,a>b,∴a·>b·,∴>,故A正确;取c=0,可排除B;取a=3,b=1,c=0,d=-4,此时a-c<b-d,故C错误;取a=3,b=1,c=-4,d=0,此时a+c<b+d,故D错误.
已知集合A={x|2<x<4},B={x|(x-1)(x-3)<0},则A∩B等于( )
解析:
∵A={x|2<x<4},B={x|(x-1)(x-3)<0}={x|1<x<3},
∴A∩B={x|2<x<3}.
若正数m,n满足2m+n=1,则+的最小值为( )
解析:
∵正数m,n满足2m+n=1,
∴+=(2m+n)=++≥+2=+,
当且仅当n=m=-1时取等号.
∴+的最小值为+.
已知p∈R,M=(2p+1)(p-3),N=(p-6)(p+3)+10,则M,N的大小关系为( )
解析:
M-N=(2p+1)(p-3)-[(p-6)(p+3)+10]=p2-2p+5=(p-1)2+4>0,所以M>N.
不等式|x|(1-2x)>0的解集为( )
解析:
因为|x|≥0,
故|x|(1-2x)>0等价于
即x<0或0<x<.
若不等式(a-2)x2+2(a-2)x-4<0对∀x∈R恒成立,则实数a的取值范围是( )
解析:
当a-2=0,即a=2时,不等式为-4<0,对∀x∈R恒成立.
当a≠2时,则即
解得-2<a<2.
综上,实数a的取值范围是{a|-2<a≤2}.
已知关于x的不等式ax2-x+c>0的解集为{x|-2<x<1},则函数y=ax2+x+c的图象为( )
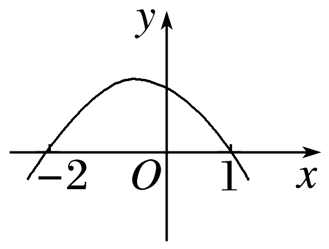
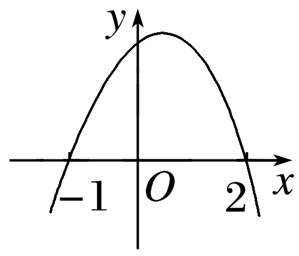


解析:
由题意可知,a<0且
∴
∴函数y=ax2+x+c=-x2+x+2的图象为B项.
已知实数x满足0<x<,则y=8x+的最大值为( )
解析:
由0<x<得到-1<2x-1<0,
则0<1-2x<1,
y=8x+=4(2x-1)++4
=-+4
≤-2+4=0,
当且仅当x=时上式取等号,
则y=8x+的最大值为0.
(多选)若实数a,b满足1<a<3,2<b<7,则下列结论中正确的有( )
解析:
因为1<a<3,2<b<7,所以3<a+b<10,2<ab<21,故A,C正确;
因为1<a<3,所以-3<-a<-1,又2<b<7,所以-1<b-a<6,故B错误;
因为1<a<3,所以<<1,又2<b<7,所以<<7,故D错误.
(多选)已知正实数x,y满足x+=4,下列说法正确的是( )
解析:
∵x>0,y>0,x+=4,
∴4->0,解得y>,∴0<x<4.
x+≥2,即4≥2,
解得0<≤2(当且仅当x=2,y=1时取最大值2),故A正确;
x-y=4--y=4-≤4-2(当且仅当y=,x=4-时取最大值4-2),故B错误;
当x=,y=时,满足x+=4,此时xy=1,故C错误;
+y=×=≥2(当且仅当x=2,y=1时取最小值2),故D正确.
(多选)对于给定实数a,关于x的一元二次不等式(ax-1)(x+1)<0的解集可能是( )
解析:
当a>0时,解得-1<x<;
当a=0时,解得x>-1;
当-1<a<0时,解得x<或x>-1;
当a=-1时,解得x≠-1;
当a<-1时,解得x<-1或x>.
关于x的不等式>0,若此不等式的解集为,则m的取值范围是 .
答案: m<0
解析:
由>0,得(mx-1)(x-2)>0,
因为不等式(mx-1)(x-2)>0的解集为,
所以即m<0,
所以m的取值范围是m<0.
已知x>0,y>0,2x+3y=6,则xy的最大值为 .
答案:
解析:
因为x>0,y>0,2x+3y=6,
所以xy=(2x·3y)≤·=×=.
当且仅当2x=3y,即x=,y=1时,xy取得最大值.
某种衬衫进货价为每件30元,若以40元一件出售,则每天能卖出40件;若每件提价1元,则每天卖出件数将减少一件,为使每天出售衬衫的净收入不低于525元,则每件衬衫的售价的取值范围是 .(假设每件衬衫的售价是m)
答案: {m|45≤m≤65}
解析:
设每件衬衫提价x元,则每件衬衫的售价为(40+x)元,
则每天出售衬衫的净收入为(40+x-30)(40-x)=(-x2+30x+400)元,
由题可知,-x2+30x+400≥525,
整理得(x-25)(x-5)≤0,
解得5≤x≤25,
则45≤m≤65.
若实数x>0,y>0,且满足x+y=8-xy.
(1)求xy的最大值;
(2)求x+y的最小值.
答案: 解 (1)∵x>0,y>0,∴8-xy=x+y≥2, 即(+4)(-2)≤0,解得0<xy≤4,当且仅当x=y=2时,等号成立, ∴xy的最大值为4. (2)8-(x+y)=xy≤, ∴[(x+y)+8][(x+y)-4]≥0, ∴x+y≥4,当且仅当x=y=2时,等号成立. 即x+y的最小值为4.
设命题p:方程x2+(2m-4)x+m=0有两个不相等的实数根;命题q:对所有的2≤x≤3,不等式x2-4x+13≥m2恒成立.
(1)若命题p为真命题,求实数m的取值范围;
(2)若命题p,q一真一假,求实数m的取值范围.
答案: 解 (1)若命题p为真命题,即方程x2+(2m-4)x+m=0有两个不相等的实数根, 则有Δ=(2m-4)2-4m=4m2-20m+16>0, 解得m<1或m>4. ∴实数m的取值范围为{m|m<1或m>4}. (2)若命题q为真命题,则对所有的2≤x≤3,不等式x2-4x+13≥m2恒成立. 设y=x2-4x+13,只需2≤x≤3时,m2≤ymin即可. ∵y=x2-4x+13=(x-2)2+9,2≤x≤3. ∴ymin=9,∴m2≤9,解得-3≤m≤3. ∴当命题q为真命题时,实数m的取值范围为{m|-3≤m≤3}. ∵命题p,q一真一假, ∴若命题p为真命题,命题q为假命题,则有 解得m<-3或m>4; 若命题p为假命题,命题q为真命题,则有 解得1≤m≤3. 综上所述,当命题p,q一真一假时,实数m的取值范围为{m|m<-3或1≤m≤3或m>4}.
(1)若关于x的不等式ax2-2x+3≤0在x∈R上有解,求实数a的取值范围;
(2)若关于x的不等式-2≤ax2-2x+3≤2恰有一个实数解,求实数a的值(或取值范围).
答案: 解 (1)①当a=0时,由-2x+3≤0,解得x≥,满足题意; ②当a<0时,令y=ax2-2x+3,则此二次函数的图象开口向下,满足题意; ③当a>0时,Δ=4-12a≥0,解得a≤, 综上所述,实数a的取值范围为. (2)当a=0时,-2≤-2x+3≤2, 即≤x≤,不满足条件,舍去; 当a≠0时,令y=ax2-2x+3, 若a>0,则函数y=ax2-2x+3的图象开口向上, ∴函数的最小值为2,∴=2,∴a=1; 若a<0,则函数y=ax2-2x+3的图象开口向下, ∴函数的最大值为-2, ∴=-2,∴a=(舍去), 综上所述,实数a的值为1.
已知a,b,c均为正数,a,b,c不全相等.若abc=1,证明:++<++.
答案: 证明 ∵a,b,c是不全相等的正数,且abc=1, ∴++=++=++, ∵2≤+,当且仅当b=c时取等号, 2≤+,当且仅当a=b时取等号, 2≤+,当且仅当a=c时取等号, ∴以上三个不等式中至少有一个等号不成立, ∴2+2+2<2, 即++<++, ∴++<++.
国际上钻石的重量计量单位为克拉.已知某种钻石的价值(美元)与其重量(克拉)的平方成正比,且一颗重为3克拉的该钻石的价值为54 000美元.
(1)写出钻石的价值y关于钻石重量x的关系式;
(2)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为m克拉和n克拉,试证明:当m=n时,价值损失的百分率最大.
(注:价值损失的百分率=×100%;在切割过程中的重量损耗忽略不计)
答案: (1)解 由题意可设价值与重量的关系式为y=kx2(x≥0), ∵3克拉的钻石的价值是54 000美元, ∴54 000=k·32,解得k=6 000, ∴y=6 000x2, ∴此钻石的价值与重量的关系式为 y=6 000x2(x≥0). (2)证明 若两颗钻石的重量分别为m,n克拉, 则原有价值是6 000(m+n)2, 现有价值是6 000m2+6 000n2, 价值损失的百分率为×100%=×100%≤=, 当且仅当m=n时,等号成立. ∴当m=n时,价值损失的百分率最大.