如图,U为全集,M,P,S是U的三个子集,则阴影部分所表示的集合是( )
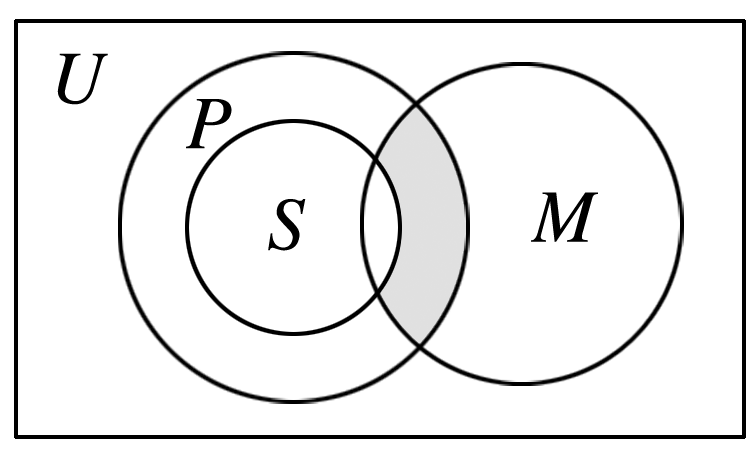
- A: (M∩P)∩S
- B: (M∩P)∪S
- C: (M∩P)∩(∁US)
- D: (M∩P)∪(∁US)
解析:
题图中的阴影部分是M∩P的子集,不属于集合S,属于集合S的补集,即是∁US的子集,则阴影部分所表示的集合是(M∩P)∩(∁US).
已知集合U={1,2,3,4,5,6,7,8},A={2,5,6},则∁UA等于( )
解析:
集合U={1,2,3,4,5,6,7,8},A={2,5,6},
故∁UA={1,3,4,7,8}.
已知集合A={x|-2<x<3},B={x∈N|-1<x≤3},则A∩B等于( )
解析:
因为A={x|-2<x<3},集合B={x∈N|-1<x≤3}={0,1,2,3},
所以A∩B={0,1,2}.
已知非空集合A={x|2-a<x<1+3a},集合B={a},B⊆A,则实数a的取值范围是( )
解析:
由B⊆A可知B是A的子集,
结合数轴可知,2-a<a<1+3a,
即解得a>1.
集合A,B满足A∪B={1,3,5,7,9},A∩B={1,7},A={1,5,7},则集合B中的元素个数为( )
解析:
由集合A,B满足A∪B={1,3,5,7,9},
因为A∩B={1,7},可得{1,7}⊆B,
又因为A={1,5,7},可得5∉B,
因为A∪B={1,3,5,7,9},所以B={1,3,7,9},即集合B中的元素个数为4.
如图,U为全集,M,P,S是U的三个子集,则阴影部分所表示的集合是( )

解析:
题图中的阴影部分是M∩P的子集,不属于集合S,属于集合S的补集,即是∁US的子集,则阴影部分所表示的集合是(M∩P)∩(∁US).
(多选)已知a,b∈R,集合{a,b,1}与集合{a2,a+b,0}相等,下列说法正确的是( )
解析:
根据题意,a=0或b=0,
当a=0时,a2=0,不符合题意;
当b=0时,{a,b,1}={a,0,1},{a2,a+b,0}={a2,a,0},
则a2=1,解得a=1(舍去)或a=-1,
所以a=-1,b=0,a2 024+b2 024=1.
(多选)已知集合{x|(x-a2)(x-1)=0}的元素之和为1,则实数a所有可能的取值为( )
解析:
因为集合{x|(x-a2)(x-1)=0}的元素之和为1,
所以当一元二次方程(x-a2)(x-1)=0有两个相等实根时,可得x=a2=1,即a=±1;
当方程有两个不相等实根时,x=a2=0,即a=0,
综上,实数a 所有取值的集合为{0,1,-1}.
(多选)已知两个数集A和B,定义A-B={x|x∈A,x∉B},AΔB=(A-B)∪(B-A).则下列命题正确的有( )
解析:
AΔB=(A-B)∪(B-A)={x|x∈A,x∉B或x∈B,x∉A},BΔA=(B-A)∪(A-B)={x|x∈B,x∉A或x∈A,x∉B},则AΔB=BΔA成立,故A正确;BΔ(BΔA)={x|x∈A,x∈B或x∈A,x∉B}=A,AΔ(AΔB)={x|x∈A,x∈B或x∈B,x∉A}=B,则AΔ(AΔB)=BΔ(BΔA)不一定成立,故B错误;令A=B={1,2},则AΔB=∅,故C正确;令A={x|x>1},B={x|x≤1},则AΔB=R,故D正确.
集合A={5,a+3},B={a2+1,a,a+1},若A∩B={2},则实数a= .
答案: -1
解析:
因为A∩B={2},则2∈A,
所以a+3=2,a=-1,此时B={2,-1,0}满足题意.
已知-3∈{12,a2+4a,a},则实数a=.
答案: -1
解析:
若a=-3,则a2+4a=9-12=-3,不符合集合元素的互异性,舍去;
若a2+4a=-3,则a2+4a+3=0,可得a=-1或a=-3(舍去),
所以a=-1,此时集合为{12,-3,-1}.
已知全集U={x|x取小于20的质数},且B∩∁UA={2,3},A∩∁UB={11,17},∁U(A∪B)={5},则A∩B=.
答案: {7,13,19}
解析:
∵全集U={x|x取小于20的质数}={2,3,5,7,11,13,17,19},
且B∩∁UA={2,3},A∩∁UB={11,17},∁U(A∪B)={5},
∴由Venn图可知A={11,17,7,13,19},B={2,3,7,13,19},
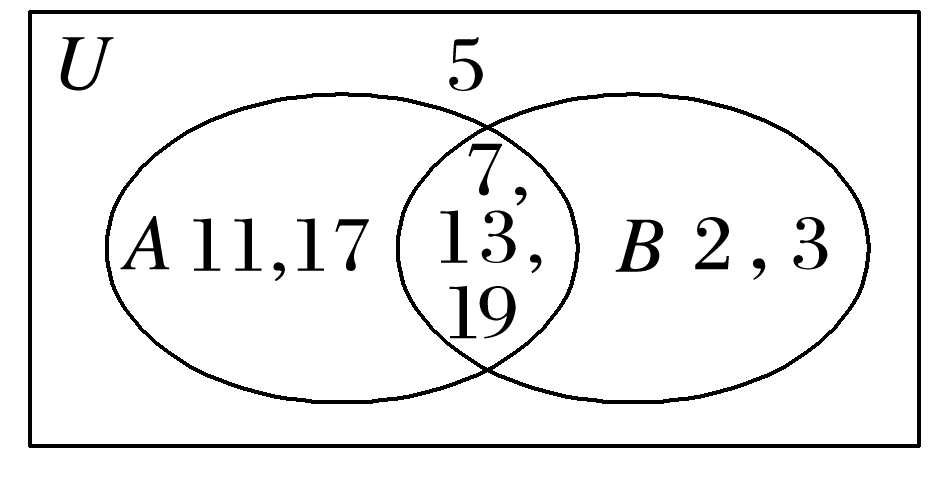
∴A∩B={7,13,19}.
若集合A={x|x2-5x+6=0},B={y|my+2=0},若满足A∪B=A的所有m的值组成的集合记为Q,则Q的真子集个数为.
答案: 7
解析:
由A={x|x2-5x+6=0}可得A={2,3},
由于A∪B=A,所以B⊆A,
当B=∅时,m=0,
当B={2}时,则2m+2=0,解得m=-1,
当B={3}时,则3m+2=0,解得m=-,
所以Q=,
故Q的真子集个数为23-1=7.
已知全集U=R,A={x|-1≤x≤4},B={x||x|≤2},P=.
(1)求A∪B,A∩B;
(2)求(∁UB)∩P.
答案: 解 (1)由B={x||x|≤2},可得B={x|-2≤x≤2}, ∵A={x|-1≤x≤4}, ∴A∪B={x|-2≤x≤4},A∩B={x|-1≤x≤2}. (2)∁UB={x|x<-2或x>2}, (∁UB)∩P=.
已知集合A={x|ax2-2x+1=0,a∈R}.
(1)若A是空集,求实数a的取值范围;
(2)当B={x|x>0}时,若A∩B为非空集合,求实数a的取值范围.
答案: 解 (1)若A是空集,则方程ax2-2x+1=0无实根, 当a=0时,-2x+1=0, 解得x=,不符合题意. 所以a≠0,Δ=4-4a<0,解得a>1. 故实数a的取值范围为{a|a>1}. (2)当B={x|x>0}时,A∩B≠∅. 所以方程ax2-2x+1=0至少有一个正实根. ①当a=0时,-2x+1=0,解得x=, 所以A∩B=,符合题意. ②当a≠0时,由Δ=4-4a≥0,则a≤1且a≠0. 当a=1时,A={x|x2-2x+1=0}={1}. 此时A∩B={1},符合题意. 当a<1且a≠0时,方程ax2-2x+1=0有两个不相等的实根, 且方程ax2-2x+1=0有两正根或一正根和一负根. 所以或 解得0<a<1或a<0. 综上,实数a的取值范围为{a|a≤1}.
已知集合U=R,M={x|x≤-5或x≥8},N={x|a-1≤x≤2a+1}.
(1)若a=5,求(∁UM)∩N;
(2)若M∩N=N,求实数a的取值范围.
答案: 解 (1)当a=5时,N={x|4≤x≤11}. 又M={x|x≤-5或x≥8}, ∴∁UM={x|-5<x<8}. 因此(∁UM)∩N={x|4≤x<8}. (2)由M∩N=N,知N⊆M. 当N=∅时,a-1>2a+1, ∴a<-2,满足N⊆M. 当N≠∅时,2a+1≥a-1,则a≥-2. 要使N⊆M,则2a+1≤-5或a-1≥8, 解得a≤-3或a≥9. 又a≥-2,所以a≥9. 综上可知,实数a的取值范围为{a|a≥9或a<-2}.
已知集合P={x∈R|x2-3x+b=0},Q={x∈R|(x+1)(x2+3x-4)=0}.
(1)若b=4,存在集合M使得P为M的真子集且M为Q的真子集,求这样的集合M;
(2)若集合P是集合Q的一个子集,求b的取值范围.
答案: 解 (1)当b=4时,方程x2-3x+b=0的判别式Δ=(-3)2-4×1×4<0, 所以P=∅. 又Q={x∈R|(x+1)(x2+3x-4)=0}={-4,-1,1},故P 由已知,得M是一个非空集合,且是Q的一个真子集, 用列举法可得这样的集合M共有6个,分别为{-4},{-1},{1},{-4,-1},{-4,1},{-1,1}. (2)当P=∅时,P是Q的一个子集,此时对于方程x2-3x+b=0, 有Δ=9-4b<0,所以b>. 当P≠∅时,因为Q={-4,-1,1},所以当-1∈P时, (-1)2-3×(-1)+b=0,即b=-4, 此时P={x|x2-3x-4=0}={4,-1}, 因为4∉Q,所以P不是Q的子集; 同理当-4∈P时,b=-28,P={7,-4},也不是Q的子集; 当1∈P时,b=2,P={1,2},也不是Q的子集. 综上,满足条件的b的取值范围是.![]() Q.
Q.
对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn,则在此定义下,集合M={(m,n)|m※n=8,m,n∈N*}中的元素个数是( )
解析:
①当m,n都为正偶数时,符合条件的(m,n)有(2,6),(4,4),(6,2),共3个;②当m,n都为正奇数时,符合条件的(m,n)有(1,7),(3,5),(5,3),(7,1),共4个;③当m,n中一个为正偶数,一个为正奇数时,符合条件的(m,n)有(1,8),(8,1),共2个,所以集合M中的元素个数是3+4+2=9.
定义集合运算:A⊗B={z|z=(x+y)(x-y),x∈A,y∈B},设A={},B={1,},则集合A⊗B的真子集个数为( )
解析:
由题意知A={},B={1,},
则A⊗B中的元素有(+1)(-1)=1,(+)(-)=0,(+1)(-1)=2,(+)(-)=1四种情况,由集合中元素互异性可知集合A⊗B中有3个元素,故集合A⊗B的真子集个数为23-1=7.